8주차, K-Means Clustering and Gaussian Mixture Model

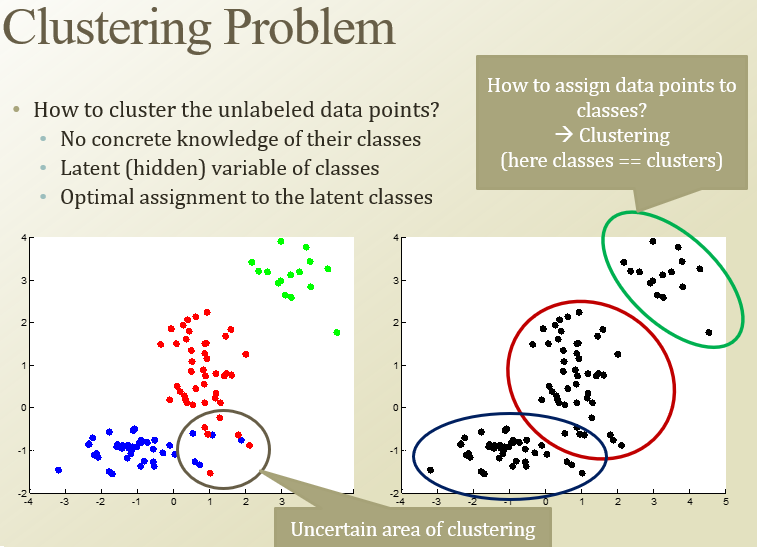
Unsupervised Learning - label 없음. 패턴을 찾는 것
K-Means
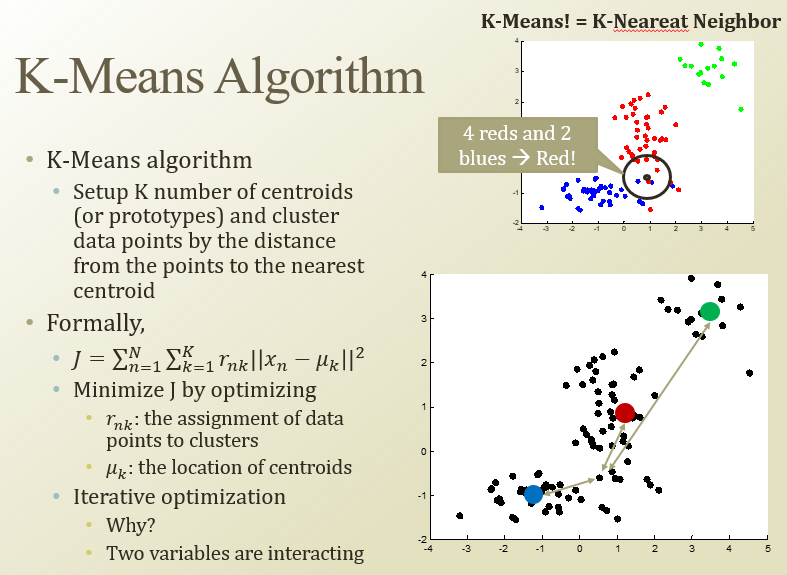
KNN이랑은 다름! KNN은 한 점에서 K개의 근처의 점을 찾아서 그 점을 판정하는거
내부 동력이 K개쯤 있다고 가정하고 분류하는 것
그리고 가까이 있는 개별 점들을 할당함
mu_k가 centroid의 위치, x가 개별 데이터. r_nk는 k번 centroid에 assign되면 1, 아니면 0
r_nk와 mu_k를 반복적으로 optimize해야함

Expectation→Maximization을 번갈아 가면서 수행하는 것
Expectation
주어진 파라미터들로 log-likelihood예측
데이터들을 가까운 centroid에 할당하는 작업(r_nk를 optimize)
Maximization
파라미터들을 최대화함.
주어진 점들로 Centroid 위치를 다시 계산함
r_nk는 지금 discrete한데, 현실은 마냥 그렇지많은 않음 → 에러발생가능
mu_k를 정리하면, 할당된 xn들의 평균값이 됨

mu_k를 랜덤하게 두고, r_nk만들고 update하고….

문제점
K를 어떻게 정할까? / centroid 시작점을 어떻게 잡을까? / 유클리드 거리 쓰는게 정말 좋은가? / hard-clustering : 무조건 하나로만 정해야 함
Gaussian mixture model

Multinomial Distribution은 P(X|mu)를 계산해야함

그냥 최대화면 미분해보면 되는데, 제약조건(subject)가 있어서 라그랑주 써야됨
이를 정리하면 mu_k = m_k/N이 됨
→ 다항분포에서 MLE는 (특정 선택지 선택한 개수) / 전체 개수

저기서 시그마 = covariance matrix
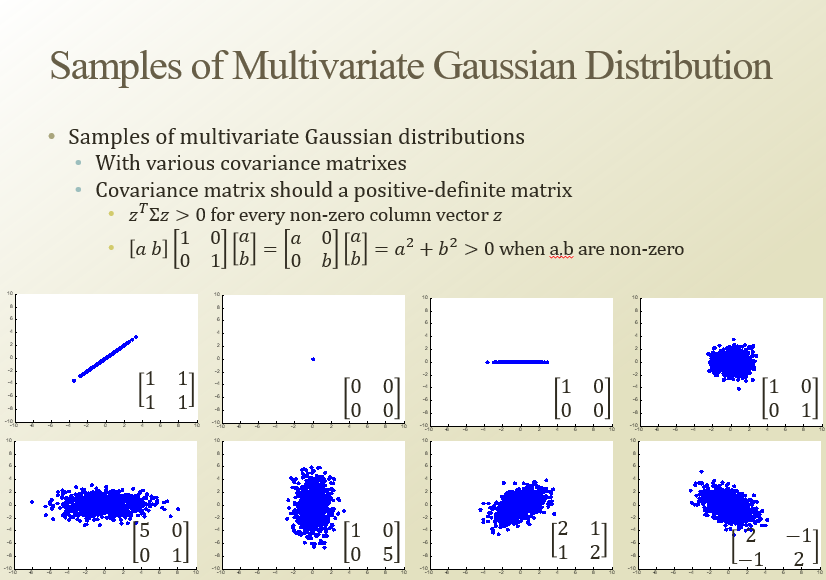
covariance matrix 에 따른 multivariate gaussian distribution
corelation에 따라 여러가지 모양이 나온다.

다항분포랑 다항 가우시안 분포를 연결시켜줘야함 → Mixture Model
맨 위 그래프를 그냥 normal로는 fitting할 수 없음(맨아래). 그래서 각각의 데이터에 대해 fitting하면 좋다.
앞에 mixing coefficient pi를 붙여서 K개의 normal을 mixing 하겠다는 것임.
이때 이 pi 정하는게 다항분포.

데이터 포인트들을 gaussian distribution으로 샘플링 하는것
K-means에서 r_nk는 0아니면 1이었다면, 여기서 z_k는 확률적(pi_k)으로 모델링됨
베이지안 네트워크 파란색 = 파라미터들
x = 관측된 것
gamma(z_nk)는 x라는 포인트가 주어졌을 때, 어떤 cluster로 들어갈지 확률
log-likelihood를 사용해서, 파라미터들(pi, mu, covariance maxtix)이 주어졌을 때 maximize하는 방향으로 optimize하겠따

E-M이 있다고 가정하고, 최적화를 해보자
사실 GMM이랑 K-means가 비슷함
Expectation step
data point를 가장 가까운 cluster에 할당햇는데, 이젠 할당할 확률 구할 수 있음
gamma(z_nk)

maximization은 파라미터(mu, sigma, pi)를 gamma(z_nk)를 활용해서 업데이트 하는거임
gamma(z_nk)가 알려져있으면, 각 파라미터에 대한 식을 구할 수 있음.
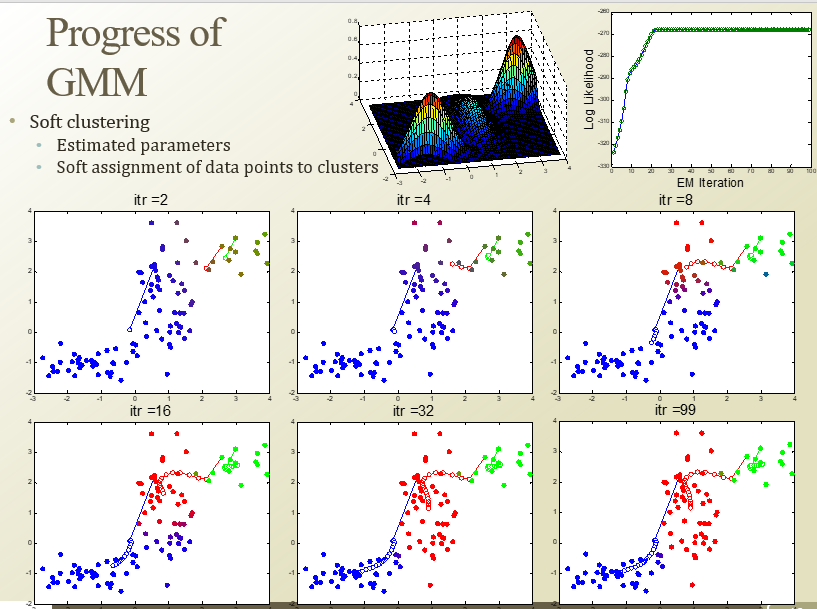
hard-margin아니어서 중간에 약간 색다른거는 반반정도란 뜻

장점
- soft-clustering
- corelation 정보도 알 수 있음 → 잠재 정보(latent factor) 더 알 수 있음
단점
- 계산 시간 오래걸림
- K를 정해야됨

covariance matrix를 eI로 가정해보자.(e는 분산 조금 조절하는 기능)
그리고 식 정리하고 e→0 하면, 나머지는 다 0인데 한 텀만 조금 남아있게됨.
이러면 hard와 비슷하게 동작함

Classification과 clustering의 차이점을 생각해보자.
X : 관측된 변수 / Z : hidden(latent) 변수 / theta = 파라미터의 분포
clustering을 해야되니까, lnP(X|theta)에서 안멈추고, summation해서 marginalize해야됨.
term들 사이에 inertaction이 존재함. 그래서 번갈아가면서 optimize

jensen’s indequality
어떤 함수가 concave()하면 내부에서 평균한거 ≥ 함수에서 나온값 평균한거
어떤 함수가 convex()하면 내부에서 평균한거 ≤ 함수에서 나온값 평균한거
log함수는 concave하다.
아까 위에 식에서 q(Z)를 임의로 곱하고 나누고, 그걸 jensen’s inequality를 통해 식을 바꿨음
그러면 뒤에 -q(Z)lnq(Z)는 entropy랑 유사함. 그러려면 q(z)가 pdf여야됨
그래서 그 Q(theta, q)함수를 최대화하는 방식으로 optimize 한다.

정리해보면, 양변에 lnP(X|theta)가 둘다 나와서, inequality를 만드는 식을 정리할 수 있음.
근데 그 식이 KL-divergence랑 비슷하게 생김. KL(P||Q) 처럼 표현함

P랑 Q2는 차이가 작고, P와 Q1은 매우 큼

그래서, KL-divergence를 0으로 만들면 maximize 되겠구나!
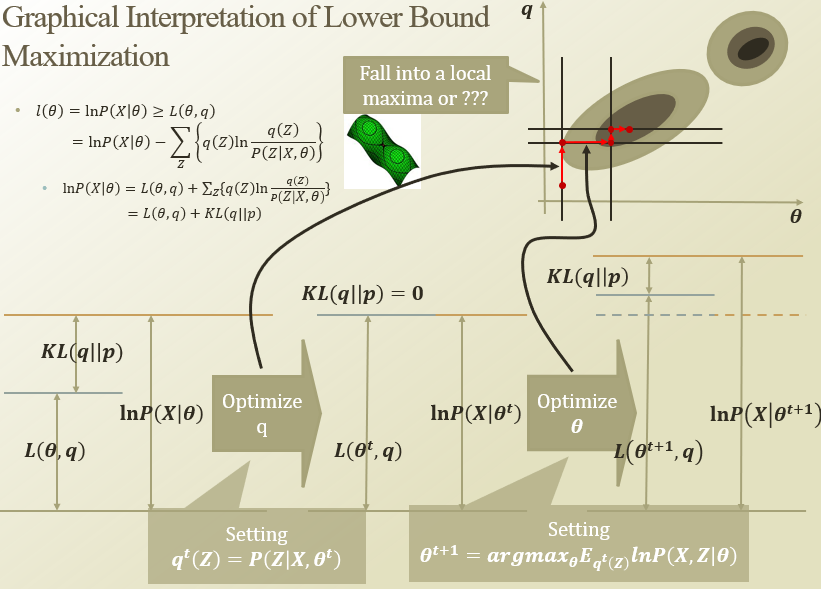
- KL-divergence를 0으로 만들어서(optimize q) equality를 만듬
- q가 바뀌어서 theta를 다시 optimize하면, KL-divergence가 바뀜
- 다시 KL-div를 0으로 만들어서… 반복

처음에 theta를 막 잡고
- expectation stepKLdiv를 최소화하는 q를 찾음
- maximization stepq가 optimize되어있어서 Z가 고정되어있음. 그래서 theta만 업데이트하면됨

EM알고리즘으로 최적화 했다…