
relative한 빈도다.

conditional prob 와 joint prob간의 관계.

joint distribution을 알면, 다양한 확률들을 알아낼 수 있다.

joint probability를 conditional probability로 계속 나눠서 곱셈 꼴로 나타내는걸
chian rule이라고 한다.

independent 하기 떄문에 곱셈으로 표현하기 쉬움
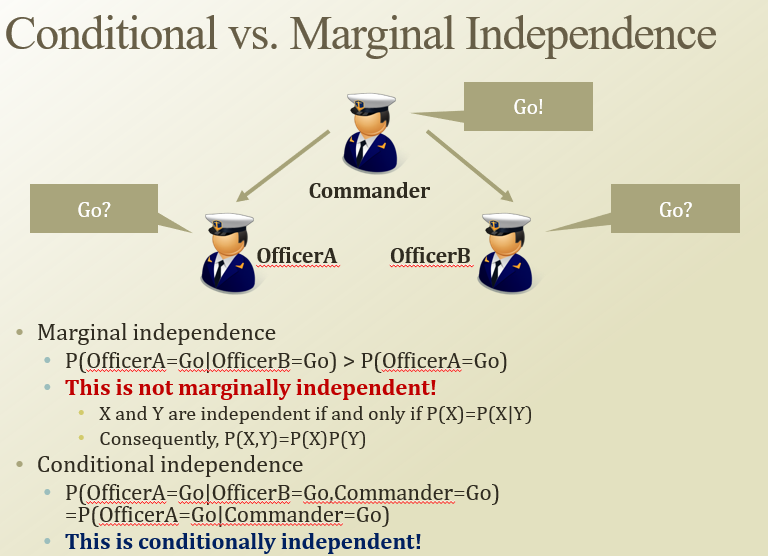
marginal : 그냥 우리가 생각하는 독립. P(X) = P(X|Y)
conditional : C가 주어지면, B에 대해서 독립(P(X|B,C) = P(A|C))
Baysian Network

conditional independent 가정해서 만듬.
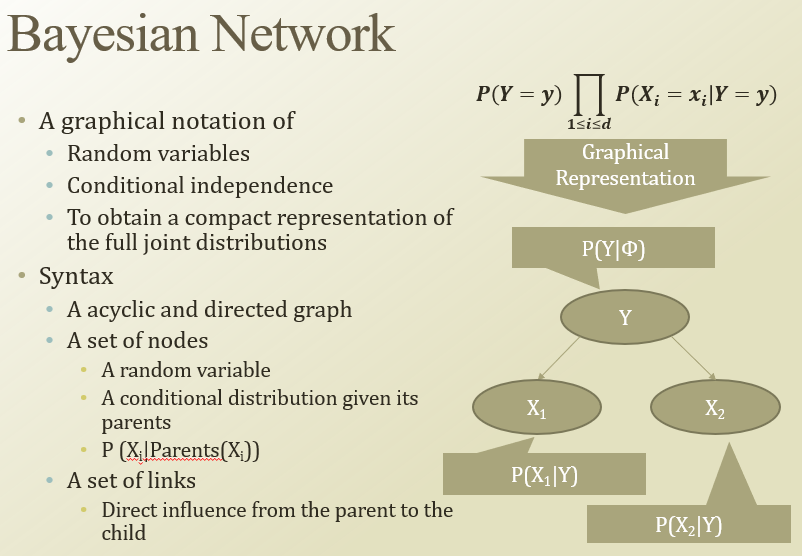
RV간의 conditional independence, RV의 full-joint distribution을 표현할 수 있는 graphical notaion.
acyclic(cycle 없는), directed(방향성) 그래프.
node : RV. P(Xi|parent(Xi))를 나타냄
link : direct influence.

conditional independencer가 어떻게 전해지는지
ex) 날씨는 toochache랑 관련이 없음
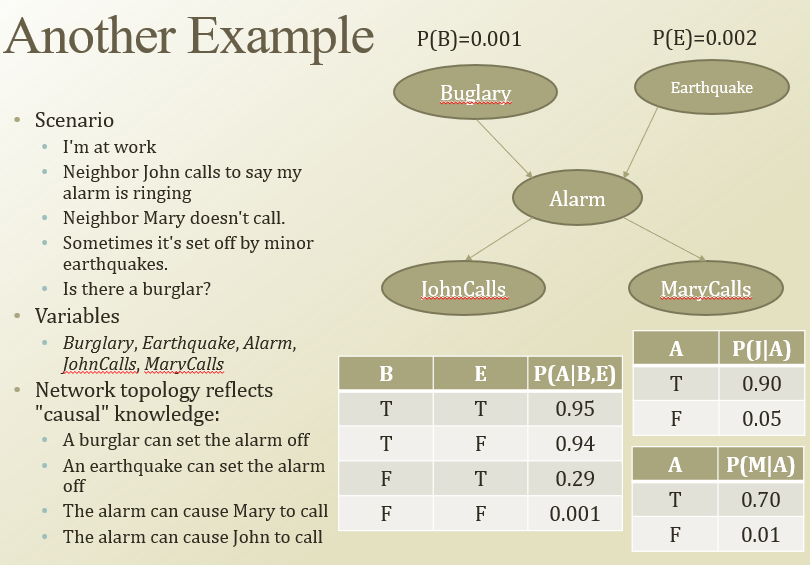
도둑/지진에 알람 울리면 johne이나 mary가 가끔 나에게 전화함.

구조 차원의 정보, 수치 측면의 정보가 동시에 쓰인다
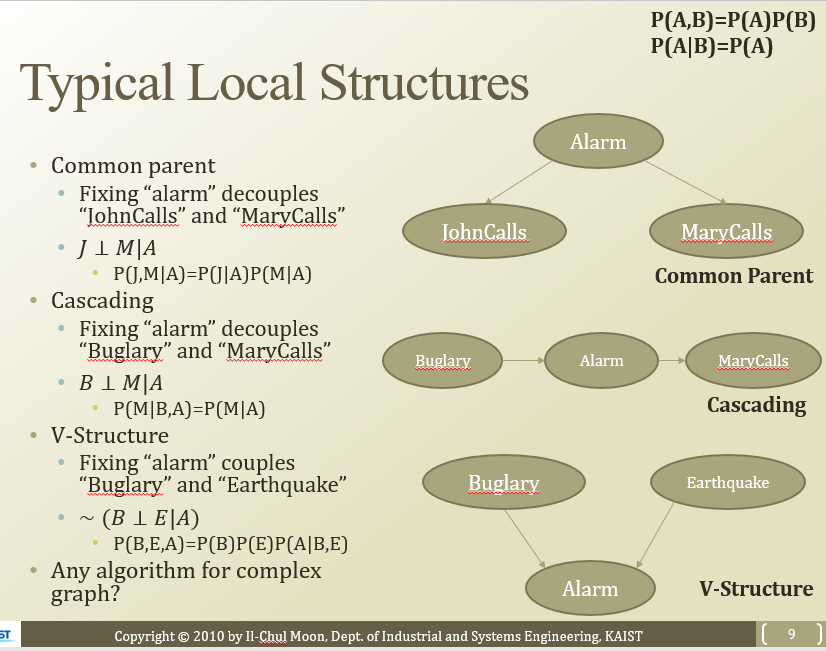
세부 구조는, 일반화된 정형화된 형태가 있음.
- common parent(공통 조상) : parent가 given이면 두 자식이 indepenent
- cascading(상속) : A(중간)이 주어지면 B랑 M 독립
- V-Structure(두 node가 같은 자식을 가짐) : A가 주어졌을 때, B랑 E가 독립이 아님
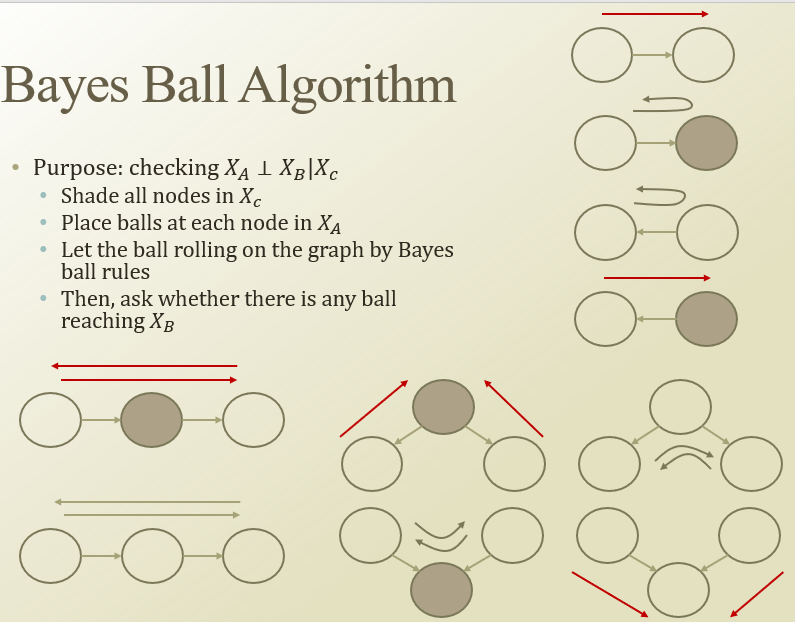
: 이 상황에서 어떤 두 node가 독립일까? 를 판단할 때 쓰임
색칠된 노드가 관측이 된 거라고 해보자.
어떤 노드에서 다른 노드로 공을 굴리다(이어져나가면) 다른 노드까지가면 독립이 아님. (앞의 3개의 sturcture에 따라서)
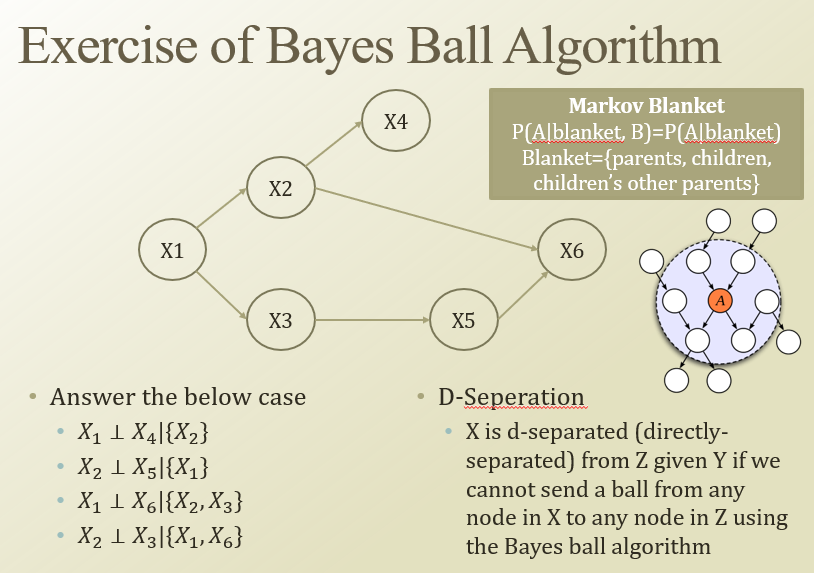
: 모든 다른 RV와 독립되게 하는 node들. blanket = {parent, childrern, children’s parents}
D-Seperation(directly seperated) : 이것도 Y가 주어졌을 때, X랑 Z가 독립이라는말
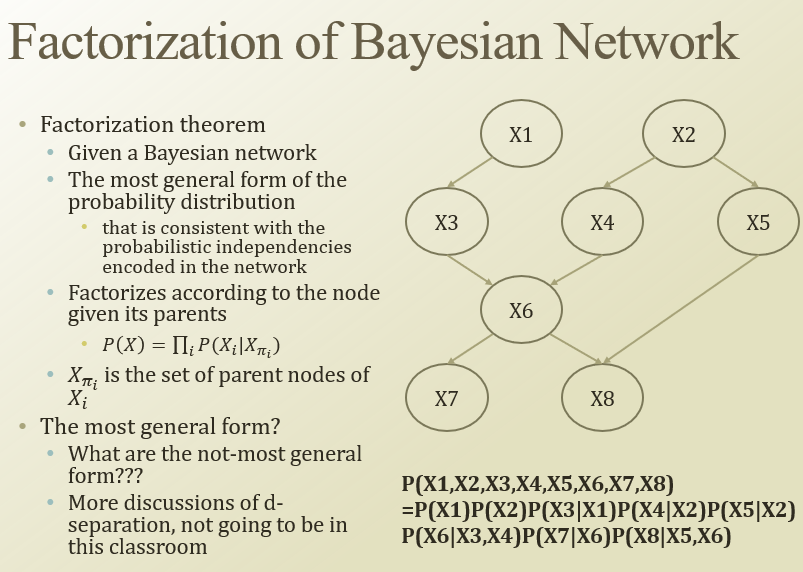
joint를 알면 conditional같은걸 알 수 있었음.
근데 joint는 parameter수가 너무 많고, 줄일려면 independent해야함
그래서 independent를 알면, factorization을 잘 해서 parameter수를 많이 줄일 수 있음(우하단 식)
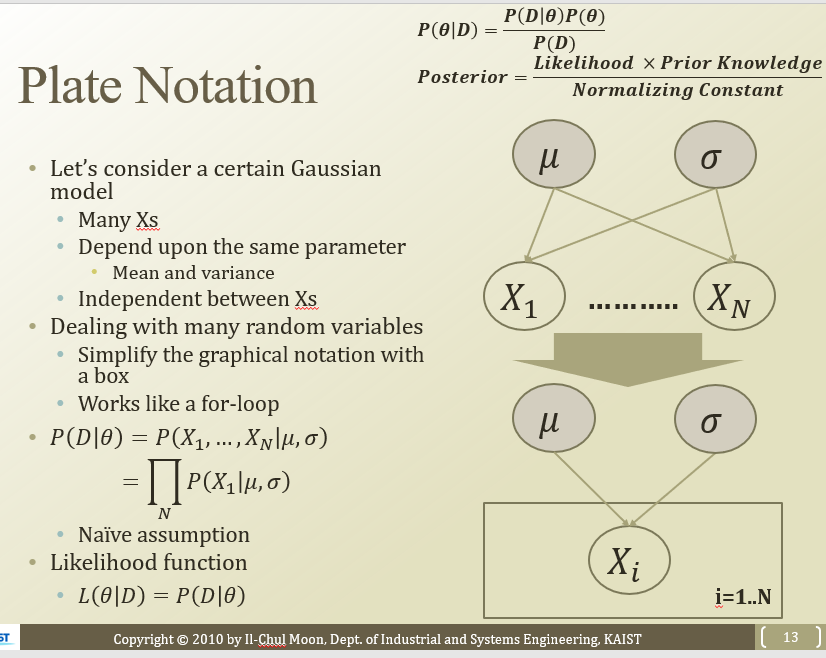
베이지안 네트워크에 “네모”라는 문법을 추가한 것
똑같은 direct관계를 가진 node들을 묶어서 쓰겠다.

X = 네트워크에 있는 모둔 RV
Xv = evidence variable(관측한)
Xh = X-Xv
일 때, P(Xv)는 모든 확률의 joint에서 Ph를 marginalize 하는것
그래서 일부분 joint를 구할 수 있음

Xh중에 관심있는 이벤트를 Y라고 하자
그걸 P(Y|Xv)로 구할 수 있다
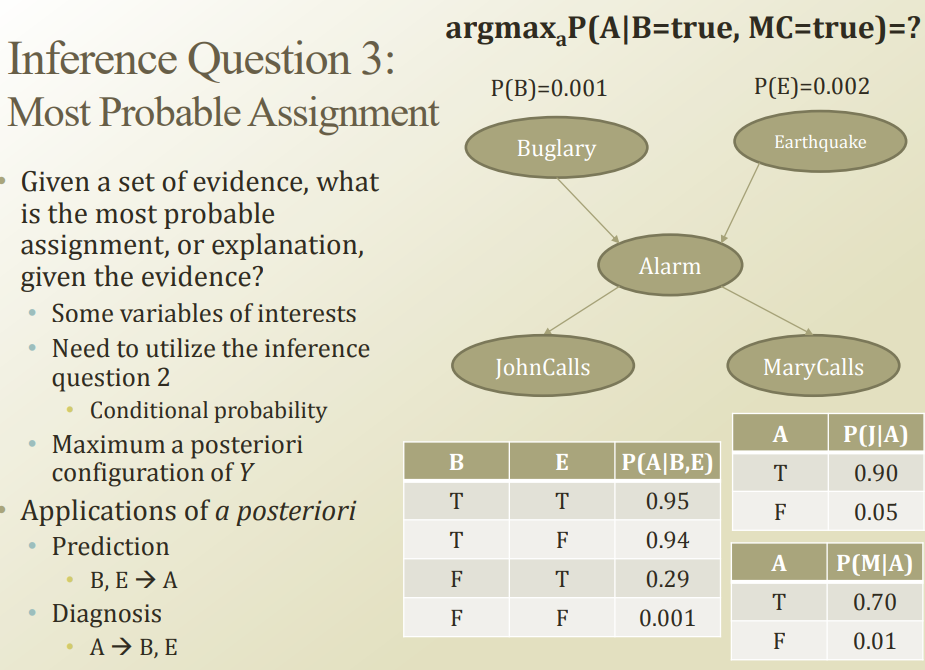
가장 말이되는 assignment가 뭘까?(=B 랑 MC있을 때 A를 어떻게 판단할까?)
이전 슬라이드의 conditional probability를 활용하면 됨

Full-joint구한다음에 maginaliza해야 원하는 값을 얻을 수 있음
근데 덧셈하고 곱셈 너무 많이해야됨. 다른 방법이 없을까?
summation해서 marginalize할 때, 상관없는 친구들을 밖으로 빼내자. 그럼 좀더 편함

preliminary에서 alpha는 regulization term(1/(P(jc,mc))

테이블들을 만들면서 점점 식을 줄여나갈 수 있음

Potential function : pdf만들고싶긴한데, 아직 뭔가 모자라서 잠재함수
Clique : 전체 네트워크에서 fully-connected된 서브그래프
Seperator : 공통으로 들어가있는걸로 clique 노드들을 서로 연결시킴
각 clique와 seperator에서 potential function을 잡았다고 생각해보자.
그러면 full-joint가 clique potential func다곱한거를 sep potential func로 다 나눈거임
그러면 psi(a,b) = P(A|B) …. phi(b) = 1… 이렇게 여러 가정을 해서 full-joint의 factorization이랑 동일하게 만들 수 있음

psi(A,B) = P(A,B) … 이렇게 잡으면 위처럼 assume할 수있음
만약 A과 관측이 되면, psi가 바뀌고( P(A,B) → P(A=1,B)), 그게 뒤로 전파되는것→
Belief propagationAbsorption Rule: 바꾸는 규칙(맨밑줄)

belief propagation 예시들.