중앙에 빨간 점이 시간 t에 따라서 위치가 바뀌었다고 생각해보자.
그럴 때 gaussian model이 어떻게 바뀌어야할까?
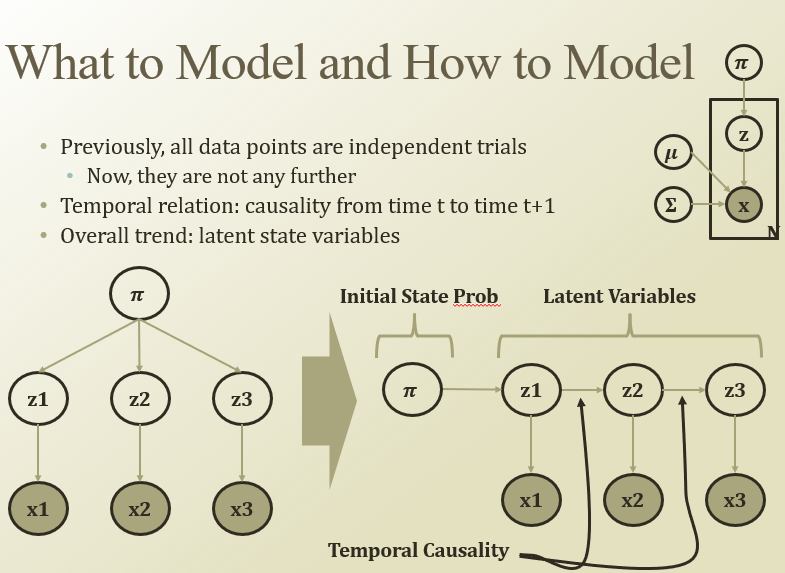
우상단 그림에서, z는 N개의 데이터 포인트가 어디에 clustering되는지 나타내는 factor
원래는 pi가 주어지면 서로 독립적이었는데, pi를 initial state로 해서 구조를 바꿈
(RNN처럼생겼네). 그래서 다음 time에 이전 거가 영향을 미친다고 모델링을 해보자.
→ Hidden Markov Model
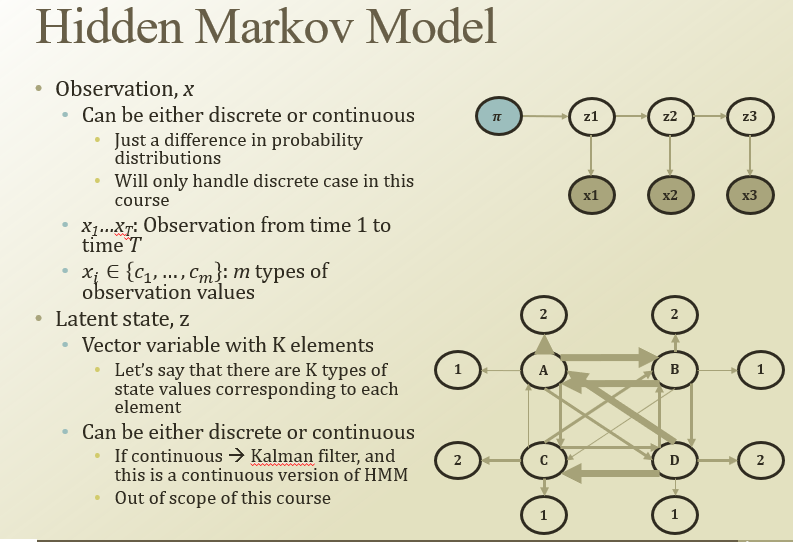
observation x는 discrete할수도 continuous할수도있음(강의에선 discrete)
x1…x_T는 1에서 T까지 시간별로 관측한 값.(x는 벡터일수도있음)
시간에 따라 K개의 cluster가 있다고 해보자. (latent factor도 continuous할 수 있음(Kalman filter))
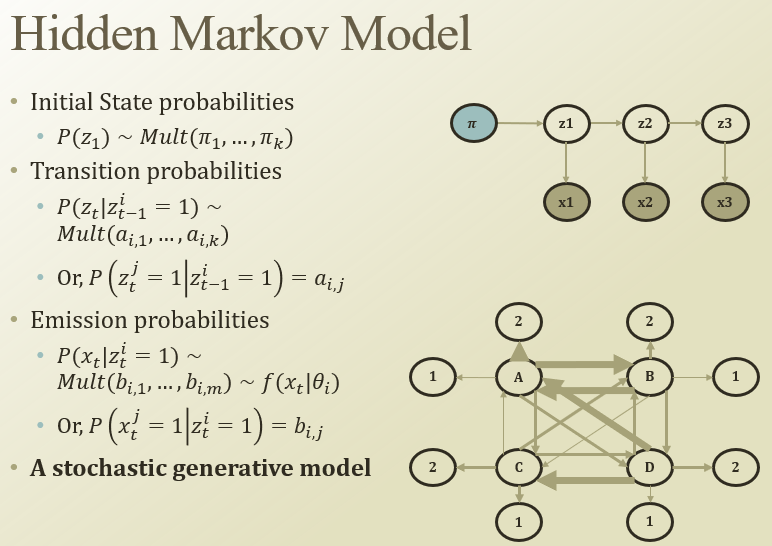
첫 latent factor인 z1은 multinomial dist.에서 샘플링됨.
Transition probability(z1 → z2, z2→z3)는 multinomial dist.로 정의할 수 있고, 파라미터를 a라고 정의해보자. (a_i,j)
Emission proabability()는 i번째 cluster에 있을 때, 어떤 x가 관측될까? → multinomial(왜냐면 discrete라고 정했으니까). 이건 b라고 정의해보자(b_i,j)
아래 그림에서 A,B,C,D는 latent factor / 1,2..는 관측되는거
- Evaluation QX를 생성했을 때, 얼마나 likely한 관측인지 평가
- Decoding Q데이터를 가장 잘 설명할 수 있는 latent factor 찾기
- Learning Q파라미터가 X밖에 없고, 주어진 데이터가 보일 확률을 가장 높일 파라미터 찾기
Eval하고 Decoding은 supervised, learning은 unsupervised로 접근 가능
속임수 주사위를 L, 진짜 주사위를 F라고 하면
LF중 뭘 던졌는지 = latent
주사위 숫자 = X
X랑 Z를 알고있다고(pi, a, b를 암) 가정하자
앞서 여러 질문(eval…)대답하려면 full-joint P(X,Z)를 알면 쉽겠다
P(X,Z)를 factorize하면 알 수 있다. factorize하면 pi,b,a로 나타낼 수 있지
full-joint marginalize하면 eval할 수 있지만, 계산이 너무 오래걸림
사실은 X만 알고 Z를 몰라서 marginal out함.
계산을 해보면, 반복하는게 되게 많음.
이걸 계산을 잘 해보면, z_t를 계산할 때, z_t-1을 알면 x_t-1까지 알 필요가 없어짐
→ recursion처럼 나타나게됨.(맨 밑 식)
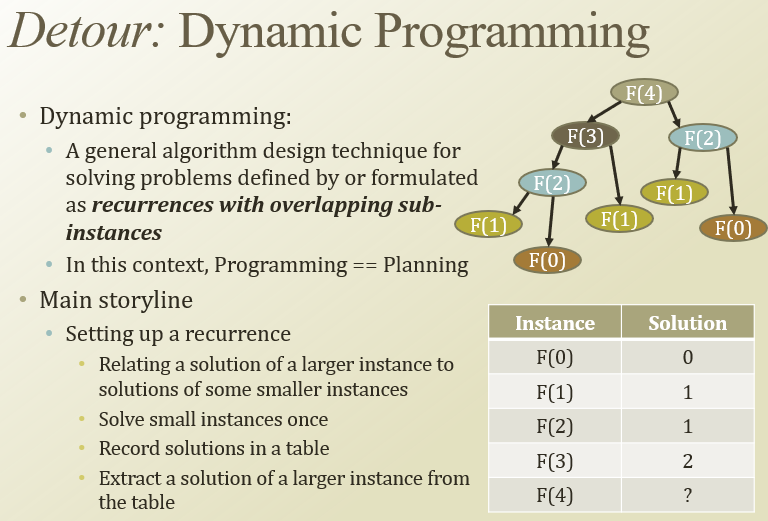
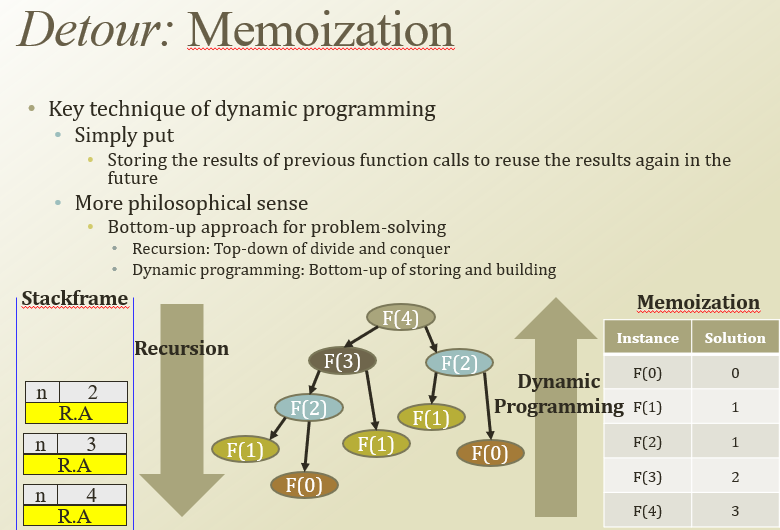
반복 계산 빠르게 하려고 DP, memoization 사용함
앞에서 구했던 alpha_t^k를 forward probability라고 하자.
맨 처음에는 initialize해서 a_1^k를 구하고, recursive로 a_t^k를 구함.
이걸 모든 클러스터에 속할 확률을 다 더하면 eval Q에 답할 수 있음
eval은 잘 할 수 있지만, alpha는 t 이전만 생각함. 미래에 있는 step을 생각 못함.
→ t를 구할 때 X 전체를 쓰고싶다 → backward probability
P(z_t^k =1 | X)를 알고싶어서 이렇게 구하는 것
backward probability도 recursive하게 만들 수 있음. (맨밑줄)
이제 이걸로 Decoding을 해볼 수 있겠다.
alpha = forward prob, beta = backward prob.
둘 다 반복되는(recursive) 구조를 가졌었음
K* = 어떤 cluster K에 대해서 가장 알맞은 assignment
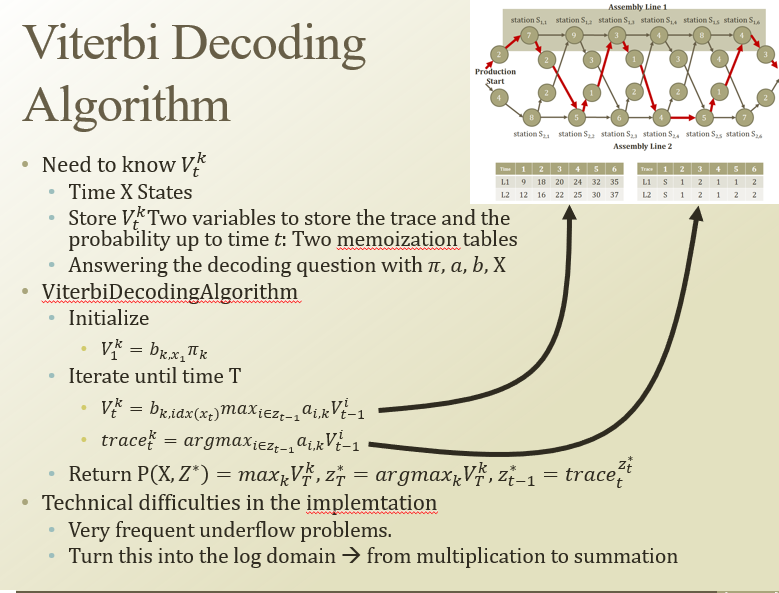
DP로 최단거리 구하는 오른쪽 상단 그림을 viterbi decoding에 적용해보자
두 개의 테이블 : trace와 특정 시간 t까지의 확률을 저장하며 따라가보자
initialize : pi를 이용해서 시작 latent state의 확률을 만듬
iteration : V를 증가시키는 방향으로 진행시킴.
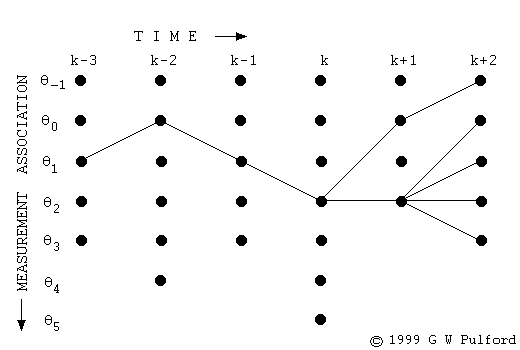https://ratsgo.github.io/data structure&algorithm/2017/11/14/viterbi/그래서 iterate를 계속 해서 V_T^K를 만들었을 때(전체 다 봤을 때) 그 K에서 뒤로 돌아가서 경로를 구하는 것
이론상으론 괜찮지만, 실제로 구현하면 underflow문제가 많이 생김(확률 곱셈을 너무 많이해서).
그래서 이걸 log domain으로 계산하기도 함
그냥 데이터 X만 엄청 모아놨을 때, 어떻게 clustering 할 수 있을까
여태 forward algorithm, viterbi decoding은 pi, a, b를 모두 알았어야했음.
K개의 cluster가 있고, X가 변할 떄, 어떻게 변하는지 dynamic clustering을 해보자.
현실에서는 X만 알고 Z, pi, a, b를 모두 다 알아내야함
어떻게 해야할까? → pi, a, b를 X로 estimate하고 가장 괜찮은 Z를 찾아내자
다시 EM으로. EM에서 theta가 HMM에선 pi, a, b임
초기 상태는 임의로 정한다
Expectation에서는 특정 time t의 정보를 가지고 Z를 assignment
Maximization에서는 Z를 활용해서 pi, a, b를 업데이트
앞서 했던대로 하면 다음 pi의 update공식을 유도할 수 있음. a,b..다
HMM의 3개의 질문 중 learning Q에 대한 답임
baum-welch는 HMM을 위한 EM 방식임(조금 디테일한)