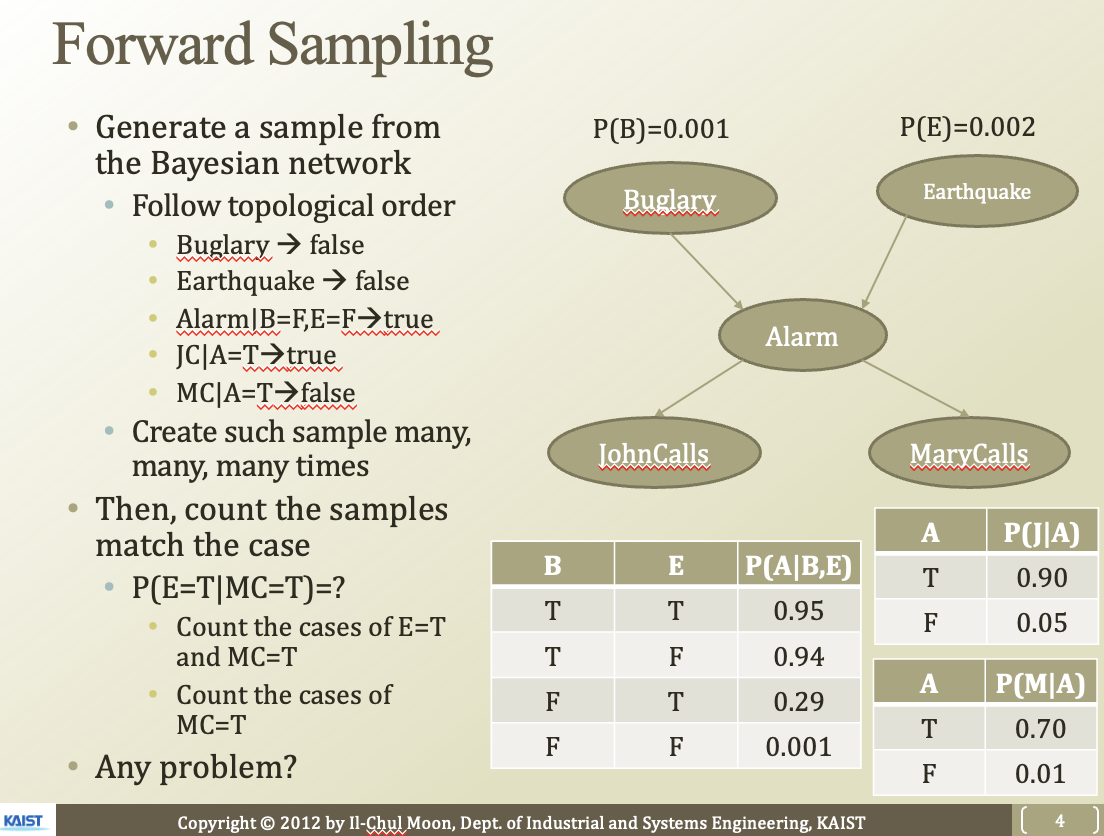
이런 베이지안 네트워크에서, topological order에 따라서 sample을 만들어 볼 수 있음. 그냥 확률값에 기반해서 한번씩 다 해보는거임
문제점
- 오차가 있을 수 있음
- 한번씩 반복하다보면 시간이 오래걸림
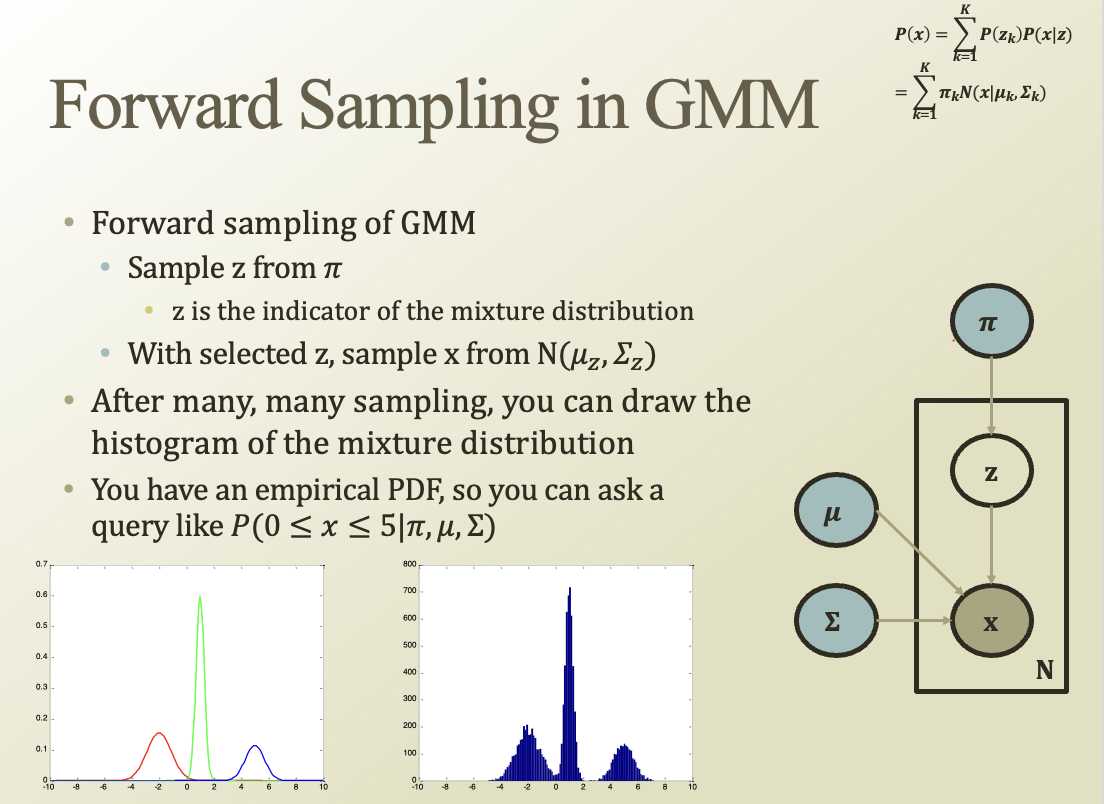
샘플링을 엄청 많이 하면, 히스토그램을 그릴 수 있을거임.
그걸 이용해서 parameter를 찾아보자는 노력임
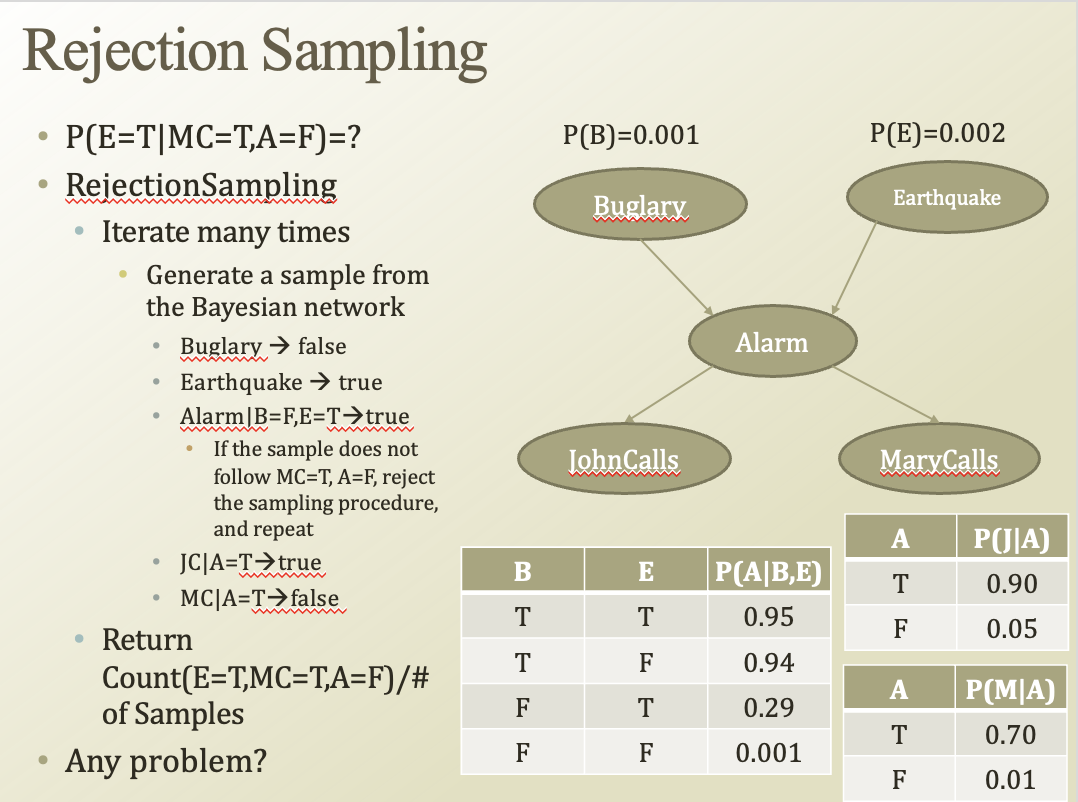
하나하나 다 해보는게 아니라 조금은 똑똑하게 해보는 것
반복을 해보다가 조건에 위배되는(알람=F가 조건인데 T라고 나오면) 그걸 더이상 진행하지 않겠다.
가지치기랑 비슷한 아이디어같음
조건을 만족한 샘플 / 모든 샘플 개수 하면 확률을 구할 수 있겠다
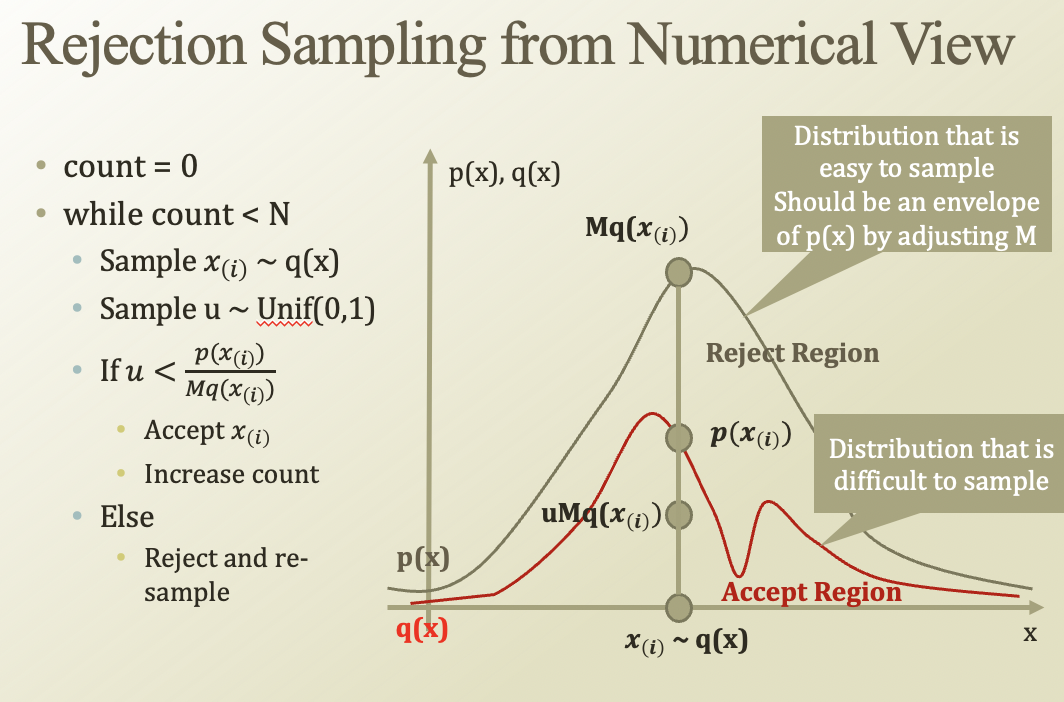
p(x(i))는 우리가 샘플링 하고싶은 분포(복잡함). 그래서 우리가 잘 알고 있는 분포에서 샘플링 하는것
q는 normal 따르고, p를 mixture dist라고 해보자.
q에다가 m을 곱해서, p의 분포를 다 덮는 Mq를 만드는거임
어떤 X에 대해서 그 값을 accept할지 말지는 p(x) / Mq(x)를 가지고 판단하겠다
그러면 Mq와 p 사이에 빈 공간만큼 reject가 될거임
문제점 : M이 덮지 못하면 동작하지 않는다. → M이 커져야됨 → 어느정도 시간이 오래걸림
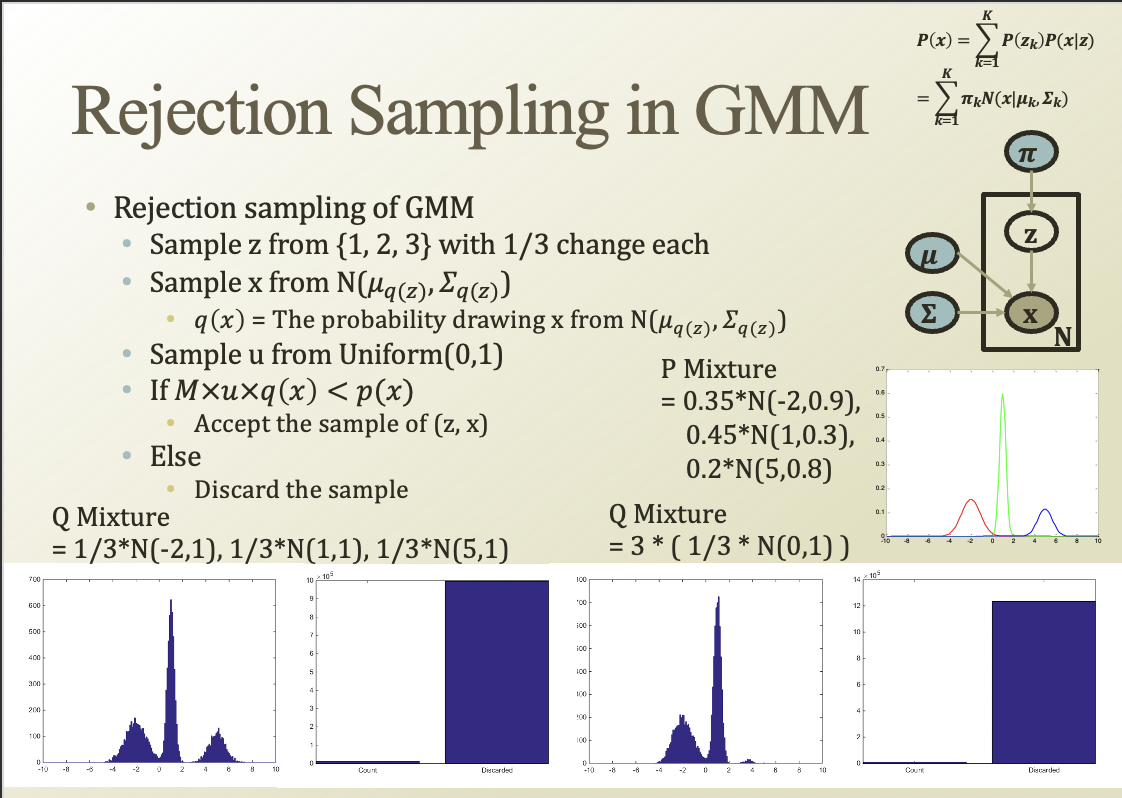
rejection sampling을 GMM으로 해보자
Normal을 여러개 붙여서 Q mixture를 만든다
오른쪽은 잘 덮고있지 않아서 undersampling됨.
실제로 잘 덮는것도 힘들고 그래서 rejectino sampling을 잘 사용하지는 않는다

그걸 보완하기 위해 쓸 수 있는게 importance sampling
우리는 히스토그램을 그리려는게 아니라, pdf의 expectation이나 확률값을 구하고 싶어하는거임
어떤 함수에 대한 기대값을 E(f)라고 해보면, 저기 시그마를 normalize하는 텀으로 사용한다. 그래서 맨뒤 시그마 뒤에 있는 식을 개별 sample의 중요도(weight)라고 볼 수 있다.
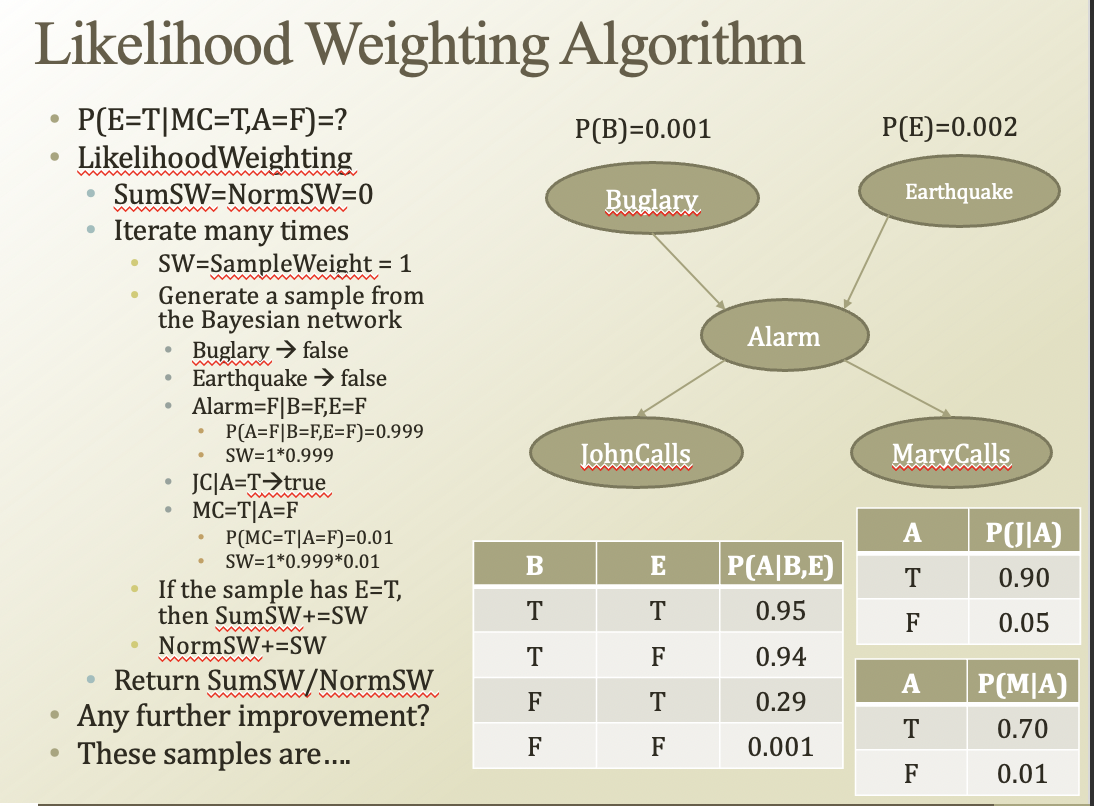
결국 importance sampling의 핵심은, 샘플링 하기 어려운 p 대신 q 분포를 이용하는 것임. Return SumSW / NormSw에서 SumSW가 p, NormSW가 q에 해당함.

EM알고리즘은 K-means, HMM등의 background였음
Expectation부분을 sampling 기반으로 해볼수 있음

Markov Chain은 t의 state와 z+1의 state의 transition이 어떤 행렬로 일어난다고 생각해보자.
각 state variable은 확률분포를 가지고있음. 그걸 계속 계산해나가는거임

Markov Chain의 특성은
- Accessiblei에서 j로 전이될 확률이 0이 아니다
- Reducibilityi랑 j가 communicate하고, i랑 j가 모두 state에 속하면 더이상 reduce할수없다
- Periodicity주기성같은게 있다. gcd=1이면 주기성은 없다
- Transience어떤 state는 reccurent하다(다시 내 state로 돌아온다). 그게 아니면 transient
- Ergodicity어떤 state가 recurrent하고 aperiodic하면, ercodic하다고 한다.

Stationary Dist.는 Markov chain의 특수 case중 하나임
RT(Return Time) : 특정 time i에서 어떤 state를 방문했을 때, 바로 다음번에 방문하는것
Limit theorem of markov chain : 체인이 irreducible하고 ergodic하면….
pi(확률분포)에 transition matrix T를 곱해도, 여전히 pi.
개별 특성에 T를 곱해도 똑같으면, Reversible하다고 하는거임.
Reversible하면, pi는 staionary dist.임(반대는 아님)

기존 샘플링 방법의 문제 : 옛날에 샘플링한걸 사용하지 않음 → 모든 샘플이 independent
inference 문제에서는 Z를 잘 assign해야됨 → 샘플링 결과로 Z assign을 해보자
기존 정보를 활용해 다음 assignment를 하는거야(z1→z2…)
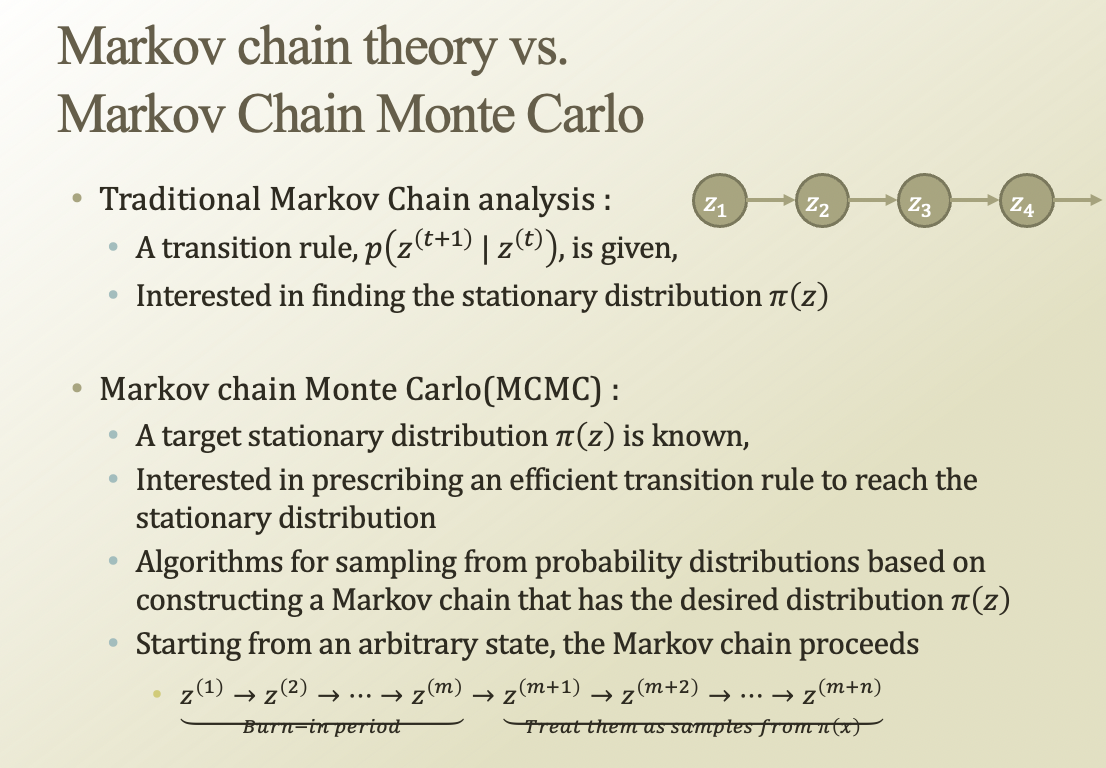
기존의 markov chain은 transitin matrix T가 주어졌을 때, stationary dist. 같은 걸 구하는데 관심이 있었음
근데, 거꾸로 생각해서 stationary dist.가 알려져있을 때 그걸 만드는 trainsition matrix를 어떻게 설명할 수 있을까? (MCMC, markov chain monte carlo)
우리가 trainsition matrix를 잘 만들어서(stationary dist.표현하게) 그걸 이용해서 매턴 샘플링을 해보자!
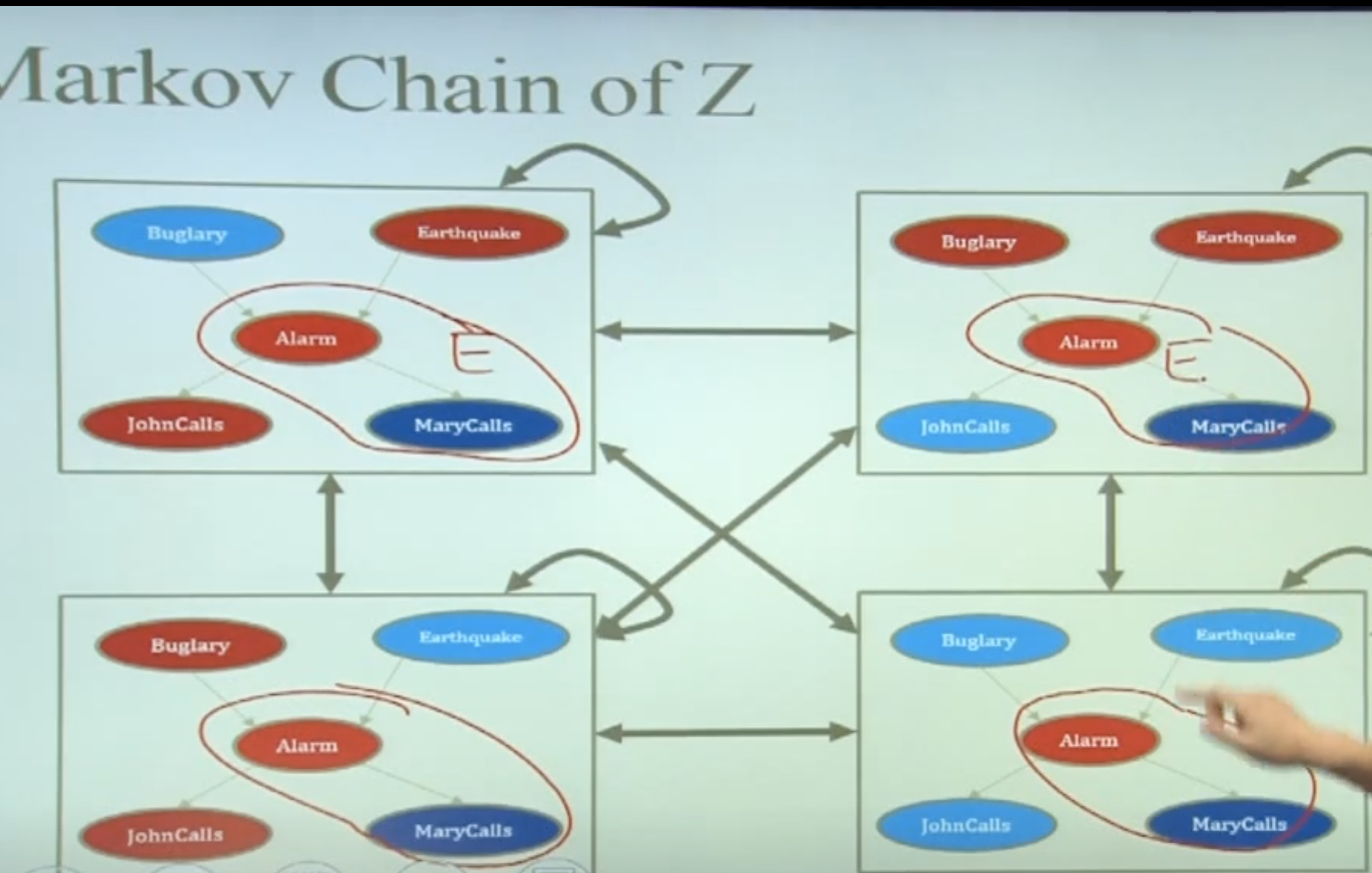
빨간 동그라미가 이미 잘 알려진 evidence라고 해보자.
처음에는 나머지를 무작위로 assign하고, 그걸 하나의 node로 생각한다.
그걸 왔다갔다하면서 assignment해보는거임
그러면 어떤 assignment는 잘 발생하고, 어떤건 잘 발생하지 않는다

Metropolis-Hasting Algorithm
MCMC에 대한 general argorithm임
어떤 assignment z가있을 때, 다음 트랜지션 뒤의 candidate z*를 제안함.
q로 trainsition하는데, 이걸 proposal dist.라고 함
acceptance prob. alpha를 정해서, z*를 alpha에 따라서 accept할지말지 정함
r(z^t|z*)가 1이 되도록 하는것임. 왜냐하면 reversible하게 만들기 위해서
그래서 min{1, r(z* | z^t)}를 alpha로 설정함

어떤 t에서 *로 갈확률을 T_t,*로 정의하고, 식으로 나타낼 수 있음(transition * accept)
그래서 결국 stationary가 되게 하는거
Random walk M-H algorithm
z*가 Normal에서 뽑혀나오고, 기존 z^t기반이라고 생각해보자.
그러고 accept까지 오른쪽 그림처럼 옮겨가고, 또 옮겨가고 하는것임
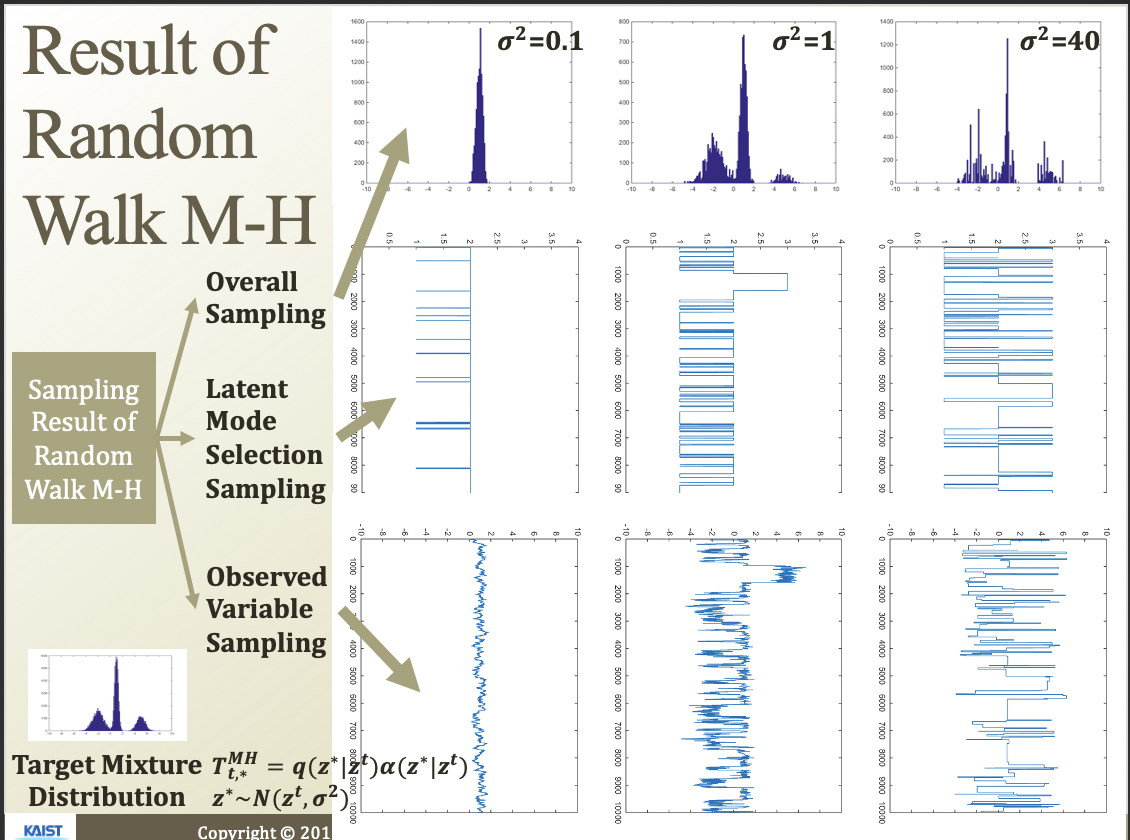
시그마에 따라서 이동이 잘 되는지 안되는지가 결정됨.
latent mode..가 z이고, observed variable …이 x라고 할 수 있음(베이지안 네트워크 그림)
지금 보면 그림따라서 샘플링이 잘 되는지 안되는지 볼 수 있음
시그마를 크게 해서 mode를 찾고, 점점 작게 하면서 정밀하게 sampling하면 좋겟네

여러 latent variable 중에 하나만(k) 해보자.
그리고 q를 새로 만들지 말고, p를 사용해보자.
그러면 balance equation을 자도으로 만족함. → accept probablity가 필요 없어짐(항상 accept)

개별 step들은 나머지를 dist에서 뽑은걸 기반으로 해서 계산한 변수를 replace하면서 진행됨.
z1 update → z2 update → z3 update 순으로 진행될거임

가운데에 likelihood가 있다고 할 때, 이런 식으로 update가될거임

latent variable들의 full joint p(z)가 있을 때, state도 zi처럼 있다고 할 때,
개별 case마다 sampling을 통해서 update하는거야
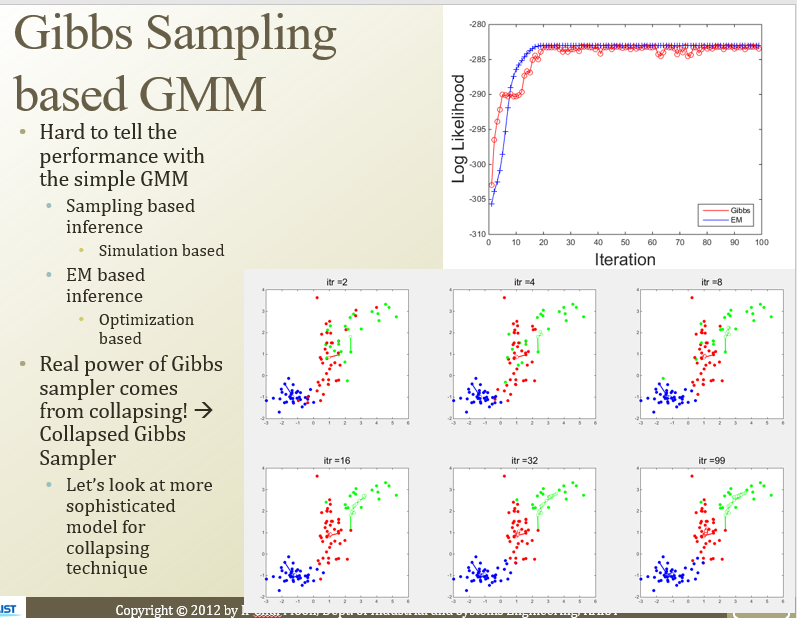
Gibbs Sampling을 GMM에 대해서 적용해볼수도있겠다
LDA
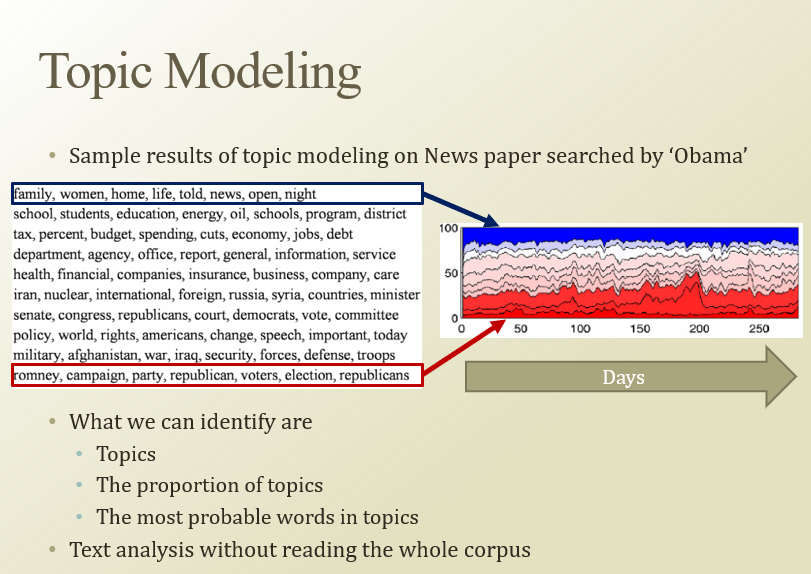
topic modeling - 단어들이 어떤 규칙에 따라서 배열해놓은것들에 주제를 알아내는거임
대용량의 문서에 modeling을 돌리면, 주제들을 찾을 수 있음(clustering)
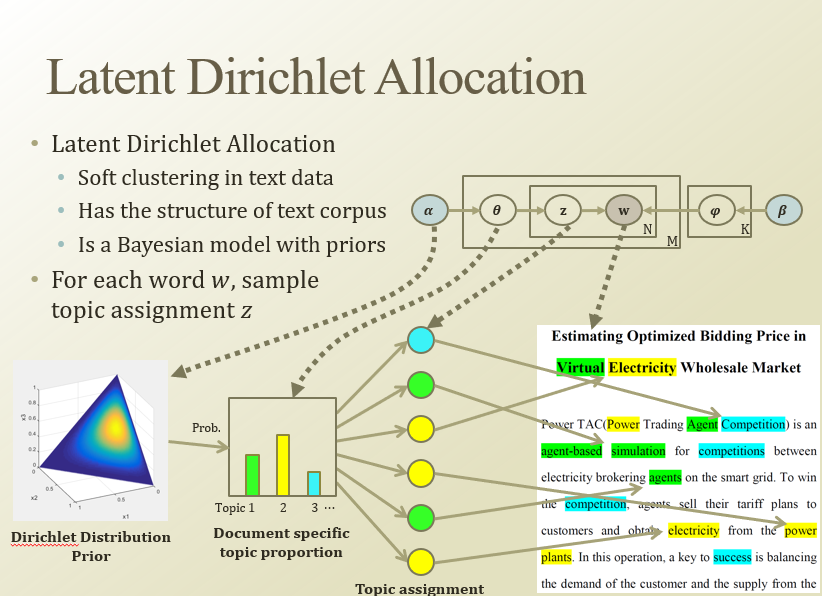
alpha, beta는 prior, w는 관측된거(신문 기사에서 단어들)
N은 한 문서에 있는 단어의 개수.
M은 문서의 개수.
theta는 문서에 대한 topic assignment. 그거에 대한 prior가 alpha.
alpha는 Dirichlet Dist. 로 모델링이 되어있음.
beta는 pi의 prior이다(K=topic의 개수)

Alram and call의 베이지안 네트워크를 생각해보자.
그걸 일반적으로 생각하는걸 Generative Process라고 한다
세타는 문서의 topic assignment가 생성된거임
세타는 그래서 개별 단어 단위 topic인 z에 대해 영향을 미침
beta→pi는 개별 단어마다 얼마나 사용할것인지 prior로 영향을 미침
그래서 그 pi로 word topic dist해서 word나옴….
Z dist가 중요하다.
w는 관측된거, alpha, beta는 prior이다.
z, theta, pi를 잘 assign하면 좋겠는데.
그럴 때, 가장 evidence에 가까운건 z다.
z를 알게되면 pi를 알 수 있게되고, theta도 estimate할수있다.
그러면 앞서 봤던 topic modeling을 할 수 있다,

그러면 z를 어떻게 잘 assign 할까 → Gibbs Sampling
어떻게? 일단 팩토라이제이션 해보자
세미콜론 : prior여서 안변한다는 뜻.( p(pi;beta) = p(pi | beta)p(beta) )
큰 PI는 plate notation들어가서 식에서 나온거임
W, Z, alpha, beta는 못없앰(w는 관측치, z는 목표, alpha beta는 prior정보 갖고있음) → theta랑 pi를 없애자
이걸 Collapsed Gibbs Sampling이라고 한다
theta랑 pi를 summation해서 없애버리자.
theta와 pi 각각에 대한 integral로 나누고, integral을 없애보자.

(1) = pi의 인테그랄 (2)=theta의 인테그랄
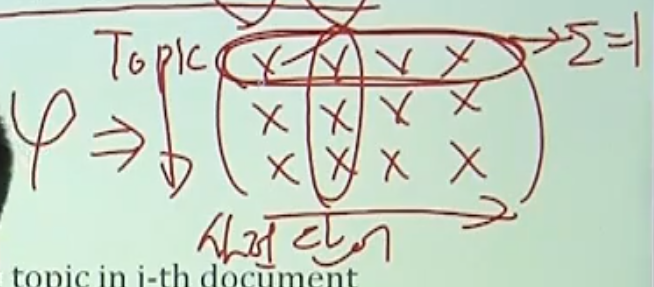
pi는 이렇게 생겼음(행렬임)

뭔가뭔가 PDF레벨로 내려가서 식 정리를 하면 뒤에거가 1이되면서…인테그랄이 사라짐

dirichlet dist랑 multinomial dist랑 곱해서 다른 dirichlet dist.가 나옴
likelihood와 prior의 곱이 prior dist 만들 때, 그 둘의 관계를 conjugate prior이라고 함
dirichlet dist는 multinomial dist의 conjugate prior임. 그래서 아주 편하게 사용될수잇음

Z를 iter하면서 나머지는 다 given인 상황에서 추림



너무 식전개라 잘 모르겠다 ㅠㅠ 여러 테크닉을 써서 식을 잘 정리한다…

TextCorpus가 문서.
nijr 구하고,
perplexity같은 성능 측정기가 converge할때까지
2중 루프를 돌면서, 다음 k를 sampling해내고, 그걸 assign하고…
Z를 이용해서 theta와 pi를 estimation함